Principio de Dualidad y Funciones Equivalentes

Principio de Dualidad

Cualquier propiedad en el álgebra de Boole sigue siendo validad si se intercambian entre si todas las operaciones (+) y (.) y además se intercambian los valores 0 y 1.

Ejemplo:

A + 0 = A
A • 1 = A

Equivalencia entre Funciones Lógicas

Dos expresiones booleanas o funciones son equivalentes si tiene igual tabla de verdad. Una expresión lógica le corresponde una sola tabla de verdad, mientras que una tabla de verdad puede formarse algebraicamente mediante diversas funciones equivalentes.

Asimismo, circuitos lógicos que corresponden a expresiones algebraicas equivalentes, o sea que realicen la misma función lógica, tendrán la misma tabla de funcionamiento por lo que podrán reemplazarse unos por otros. La equivalencia se obtiene aplicando el principio de dualidad.

Circuitos Equivalentes de un Solo Tipo de Compuertas

Equivalencias And- Or Y Nand- Nand

Es quizás la equivalencia más empleada en circuitos integrados, por ser la compuerta NAND de fabricación masiva. Algebraicamente:

Se ha convertido una suma de productos en un producto negado de productos negados

Equivalencias Or-And y Nor-Nor



de un producto de sumas se paso a una suma negada de sumas negadas.

Utilidad de las Funciones Equivalentes

Como vimos anteriormente, dos expresiones booleanas o funciones se dicen equivalentes si sus tablas de verdad coinciden. A una función lógica le corresponde una única tabla de verdad, mientras que a una misma tabla de verdad se le puede asociar diferentes expresiones equivalentes. Esto permite reemplazar un circuito por otro, dependiendo de las necesidades técnicas y/o económicas que se posean. Más especificamente, la utilidad de el concepto de funciones equivalente yace en la posibilidad de utilizar menos cantidad de chips para la implementación de un circuito. Si queremos implementar la función original Z=(P+Q).(R+S), deberíamos hacerlo:

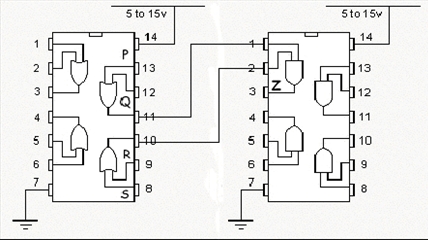
En cambio, una vez aplicado el concepto de funciones equivalentes y obtenida la expresión

la implementación mediante chips, sería:

De esta forma podemos ver que, a diferencia del primer caso, estamos utilizando sólo UN chip.