Compuertas logicas, funciones basicas y derivadas

Funciones Básicas

Expresión Booleana, Compuerta Lógica, Tabla de Verdad y Circuito Lógico

Una compuerta OR de dos entradas es un dispositivo electrónico que presenta dos entradas, a las cuales llegan los niveles de tensión de dos cables (A y B), y una salida. Esta genera en el cable (Z) un nivel que depende de los niveles existentes en las entradas. Su expresión booleana es:
Z = A + B
Esta función se puede representar mediante compuertas lógicas:

Z puede tomar 2 valores: 0 o 1. Si toma este último valor, entonces significa que Z se activa. Se debe tener en cuenta que Z = A + B, y que:

0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1


Entonces Z se activa si A o B toman el valor 1. Esto se representa con la tabla de verdad

B A Z
0 0 0
0 1 1
1 0 1
1 1 1



Las primeras dos variables A y B son las variables de entrada y Z es el resultado de la combinación de dichas variables, es decir, Z es la variable de salida. Veamos como se puede representar la función A + B con circuitos lógicos:

La corriente eléctrica, generada por la batería, debe recorrer el cable desde el polo positivo al negativo. Esto hace que se prenda la luminaria (Z = 1). Para que la electricidad pueda recorrer el cable, basta con que se active, al menos, uno de los pulsadores, es decir, A o B. En caso que ningún pulsador sea activado (A = 0 y B = 0), entonces la luminaria se encuentra apagada (Z = 0).

Convención: la posición normal de un contacto es la correspondiente al estado de reposo en que permanece, mientras no actúa ninguna fuerza venciendo a su resorte de retención. Se acostumbra designar un contacto normalmente abierto (N. A) con una variable sin negar, mientras que otro normalmente cerrado (N. C) se representa por una variable negada.

Un contacto normalmente cerrado es el que se usa el las puertas de las heladeras o automóviles, que encienden una luz cuando deja de estar oprimido.

Operación suma lógica: la compuerta or realiza una operación que simbolizaremos con el operador binario representado por el signo "+" que indica esta operación definida por la tabla de verdad anterior, la cual contempla todos los casos posibles. Se denomina suma lógica u operación Or, siendo que coincide formalmente hasta el tercer renglón de la tabla con la suma aritmética. Dado que los valores lógicos de cada suma corresponden a las variables A, B y Z, en forma sintética podemos expresar Z = A + B, y se lee Z es igual a A o B.

Compuerta OR de más de dos entradas: en una compuerta OR de un número cualquiera n de entradas a las que llegan igual número de cables designados A, B, ..., N, el cable Z conectado en su salida estará encendido si A o B o C o ... o N está encendido.

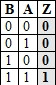
Una Compuerta AND de dos entradas es un dispositivo electrónico que presenta dos entradas, a las cuales llegan los niveles de tensión de dos cables (A y B), y una salida (Z). Su función booleana es: Z = A.B

Se debe tener en cuenta que Z = A • B, y que:

0 • 0 = 0
1 • 0 = 0
0 • 1 = 0
1 • 1 = 1


Z se activará si A y B toman el valor 1. Esto se representa con la tabla de verdad.

B A Z
0 0 0
0 1 0
1 0 0
1 1 1



Veamos como se puede representar la función A • B con circuitos lógicos:

Como se puede observar en el gráfico, la corriente eléctrica recorrerá el cable solo si se activan ambos pulsadores al mismo tiempo. Cuando esto ocurra, la luminaria se enciende. Es decir, Z se activará (Z = 1).

Operación producto lógico: a la compuerta AND la simbolizaremos con el operador binario representado por "•". Se denomina producto lógico por coincidir simbólicamente los resultados de los productos lógicos y numéricos. Puesto que los valores lógicos de cada producto corresponden a las variables A, B y Z, en forma simbólica podemos expresar: Z = A • B, y se lee Z igual a A por B.

Como en el caso de la compuerta OR, en la compuerta AND también podemos tener más de dos entradas. En ese caso, el cable Z estará encendido sólo si todos los cables de entrada están encendidos. De lo contrario, Z estará apagado.

Una compuerta seguidor es un dispositivo electrónico que actúa como buffer, es decir, que mantiene en la salida, el valor que se encuentra a la entrada. Su expresión booleana es: Z = A

A Z
0 0
1 1

Una compuerta EXOR u OR excluyente de dos entradas es un dispositivo electrónico que presenta dos entradas, a las cuales llegan los estados de las dos variables (A y B), y una salida, que genera en el cable (Z).

El comportamiento eléctrico de la compuerta XOR se resume en la siguiente tabla, que difiere de la tabla de la compuerta OR sólo en el último renglón:

A B Z
0 0 0
0 1 1
1 0 1
1 1 0


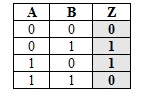
Esta compuerta es importante dado el hecho ya señalado de la imposibilidad de que un cable pueda estar con los dos estados de tensión simultáneamente. A la operación definida por esta compuerta la simbolizaremos con el operador binario representado por "(+)", y cuyas combinaciones se detallan a continuación:

Puesto que los valores lógicos de cada producto corresponden a las variables A, B y Z, podemos expresar: Z = A (+) B, y se lee Z es igual a A or excluyente B.

Compuertas Derivadas

Compuertas con un Inversor en su Salida

Compuerta NOR: una compuerta NOR es una compuerta OR con un inversor en su salida que complementa cada resultado que ésta genera, de modo de realizar una suma lógica negada.

La tabla de verdad se presenta en la figura anterior, mostrando en la última columna los cálculos algebraicos. El circuito a continuación es un circuito serie con pulsador NC:

Compuerta NAND: una compuerta NAND resulta de invertir la salida de una compuerta AND. Su expresión booleana es:

La figura muestra la tabla de funcionamiento y las operaciones algebraicas correspondientes.

Su circuito lógico es un circuito paralelo, NC:

Una Compuerta Inversor o inversora es un dispositivo electrónico que enciende el cable que está en su salida, si el cable que está en su entrada se encuentra apagado, y viceversa. Decimos entonces que los cables A y Z son complementarios, o que uno es el inverso del otro, o que están en oposición. Puede decirse que uno es la negación del otro.

Operación negación: la tabla de verdad define la operación inversión que realiza la compuerta inversora. Dado que Z vale 1 cuando A no vale 1, y que Z vale 0 cuando A no vale 0, podemos decir que Z es no A. Escribimos entonces su expresión booleana:

El símbolo de la barra sobre la variable booleana indica la operación de negación que el inversor realiza sobre los valores de la misma.

En particular, 0 = 1 y 1 = 0. Cabe mencionar que en general un círculo denota inversión, esté o no acompañado del triángulo.

Esta función se puede representar mediante compuertas lógicas:

Se debe tener en cuenta que la función inversor (o negación), justamente invierte el valor de las variables:

0 = 1
1 = 0

Entonces Z se activará si A toma el valor 0.

Veamos como se puede representar con circuitos lógicos:

Obsérvese que a diferencia de los circuitos anteriores, el pulsador aquí es normalmente cerrado. Es decir, que la corriente circula por el cable todo el tiempo (Z = 1), justamente cuando no se activa el pulsador A (A = 0).

Si se presiona el pulsador A (A = 1), entonces la electricidad dejará de recorrer el cable (Z = 0).

Una Compuerta EX – NOR (OR exclusiva negada) resulta de invertir la salida de una compuerta EX - OR. Su expresión booleana se obtiene:

Su tabla de verdad es y circuitos lógicos son:

A B Z
0 0 1
0 1 0
1 0 0
1 1 1